Asymptotic Analysis: Arithmetic Sequence

Introduction

Recently, a friend who is considering a career shift to software engineering sparked a conversation about algorithms and the analysis of runtime complexity. This friend is naturally curious, often asking “why” to understand new concepts—an admirable habit that many could benefit from adopting. In this post, I’ll delve into the runtime of a function, striving to answer as many “why” questions as possible. While I’m not an expert in mathematics, I’ll do my best to address these queries, though some may remain unanswered.

The function

The following snippet shows a nested for loop. The outer loop starts at 1 and continues through to n - 1. The inner loop is a little more interesting; it will always start at i + 1, and continue through to n (inclusive). This means the number of iterations for the inner loop depends on the current value if i.

Observing this routine, it is immediately clear that the Big O time complexity is O(n²). Simarly, Theta notation would also be (\Theta(n^2)).

void myfunction(int n) {
    int i, j;

    for (i = 1; i < n; i++) {
        for (j = i + 1; j <= n; j++) {
    }
}

Answering the First Why

How do we determine that the runtime of this routine is quadratic?

Remember that asympotic notation to analyze the runtime of an algorithm is looking at the tail behavior of the algorithm. That is, for a sufficiently large input size n, as n approaches infinity, how does my functions effort grow respective to n. When working with nested for loops, the key is to count the number of iterations; however, the number of iterations varies, because it depends on the size of n. In this case, finding the sum requires the use of a little math to find the sum of terms of an arithmetic sequence. During my original explanation, I immediately provided a well known series to show exactly why this is quadratic.

S_n = n(a₁ + a_n)⁄2

Where a₁ is the first term in the sequence, a_n is the last term, and d (not shown above) is the common difference.

Before I could procede, I was once again asked, “why?” So, before I show how to find the sum using the formula above, I’ll show why this formula even works.

Derivation of Sum of Arithmetic Series

Consider the sequence 99 + 98 + 97 + 96 + … + 1. It is quite easy to see that the common difference is -1, and that the value of a given term a_i is simply a_n = a₁ + (n - 1)d. For example, let n equal 4, then the 4^th term in this sequence, a₄, is 96. This could easily be found by taking n - 1, which is 3 and multiplying it by the common difference of -1 to give -3. Then, adding this to a₁, yields 99 + (-3) = 96.

This works well, but how did I know that the n^th term can be found using the formula a_n = a₁ + (n - 1)d? To show this, I will start by defining a few variables:

S_n = Sum of the sequence for the first n terms. d = Again, refers to the common difference between any two neighboring numbers in the sequence. a₁ = The first number in the sequence. a_n = The n^th term in the sequence.

Looking at a sequence, I can develop a pattern that will allow me to build a formula.

S_n = a + (a + d) + (a + 2d) + (a + 3d) + … + [a + (n - 1)d]

Notice that the first term a₁ begins with a and the second term increases a by the common difference, d. Makese perfect sense so far! The third term, therefore, must be 1 more than the second; however, since I’m only looking to develop a formula and don’t know what the second term is, I must use for first term a₁ or a, as a base. Every other term will calculate its value relative to the base a. Remember that there is a common difference d between two neighboring numbers in the sequence. So, the second term is simply (a + d), while the third term would be (a + d + d), or (a + 2d). That’s because it is d more than its predecessor (a + d). This pattern continues until the end of the sequence: (a + 3d), (a + 4d), …, [a + (n - 1)d]. The final term uses (n - 1) instead of an integer because we don’t know the size of the sequence.

The next step is to reverse the sum that we just defined above.

Given S_n = a + (a + d) + (a + 2d) + (a + 3d) + … + , the reversed sum is

S_n = [a + (n - 1)d] + [a + (n - 2)d] + [a + (n - 3)d] + … + a

Finally, we add the two together:

S_n + S_n = {a + [a + (n - 1)d]} + {[a + d] + [a + (n - 2)d]} + {[a + 2d] + [a + (n - 3)d]} + {[a + 3d] + [a + (n - 4)d]} + {[a + (n - 1)d] + a}

Simplifying gives:

2S_n = [a + a + (n - 1)d] + [a + d + a + (n-2)d] + [a + 2d + a + (n - 3)d] + [a + 3d + a + (n - 4)d] + [a + a + (n - 1)d] .

Each term simplifies to [2a + (n - 1)d]. To save time, I won’t simplify each one, but I’ll show how to simpify the second term, [a + d + a + (n-2)d].

[a + d + a + (n-2)d] can be written as [a + d + a + dn -2d], which becomes [2a + d + dn - 2d]. This simplifies further to [2a + dn - 1d] and factoring yields the same [2a + (n - 1)d].

We now know that each term is [2a + (n - 1)d] and given n terms, we are left with the following:

2S_n = n * [2a + (n - 1)d]. To isolate S, we simply divide by two: S_n = n * [2a + (n - 1)d]⁄2 .

Our formula is as follows:

S_n = n * [2a + (n - 1)d]⁄2

What exactly does this mean?

Remember that we want to find the sum of the first to n^th (or first to last term). Given the formula above, we consider the first element of the sequence, a₁ to be a and the n^th element, a_n to be a_n = a + (n - 1)d. Therefore,

[2a + (n - 1)d]⁄2 = a + [a + (n - 1)d] = a₁ + a_n

Finally giving, S_n = n(a₁ + a_n)⁄2

Applying this to our loop!

Looking at our original loop, we are now able to count the number of iterations for the inner and outer loop.

void myfunction(int n) {
    int i, j;

    for (i = 1; i < n; i++) {
        for (j = i + 1; j <= n; j++) {
    }
}

This snippet uses n, I don’t know when the loop will terminate. Instead, I can define a series that uses n as a relative point.

Inner loop sequence: (n - 2) + 1, (n - 3) + 1, (n - 4) + 1, …, 1 which simiplifies to:

(n - 1), (n - 2), (n - 3), … , 1

Using the formula defined earlier, we have S_n = n ((n - 1) + 1)⁄2 , which simplifies to n²⁄2. The dominant term is clearly n², which is how we know that the nested loop above is O(n²) and grows quadratically with n.

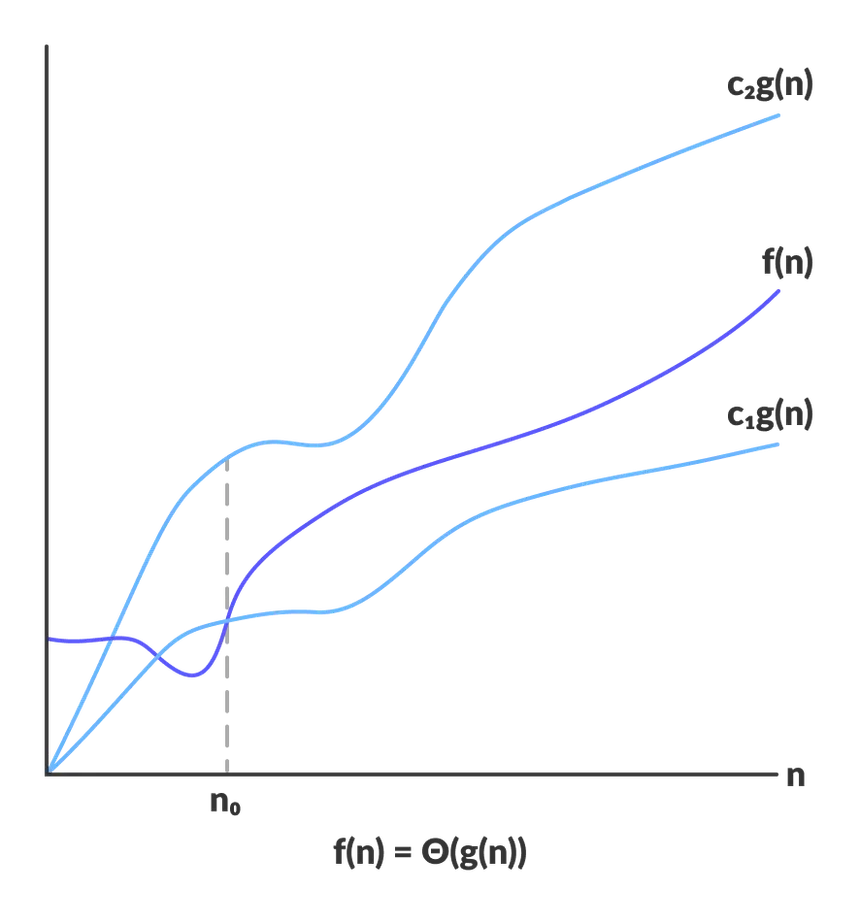
Theta Notation

The functional definition of Theta notation is: \Theta(g(n)) = f(n) ∃ c₁, c₂ >= 0 and n₀ such that 0 <= c₁ * g(n) <= f(n) <= c₂ * g(n) ∀ n >= n₀.

Upper Bound

T(n) = n²⁄2 <= n²⁄2 so I can choose 1⁄2 for c₂

Lower Bound

T(n) = n²⁄2 >= n²⁄4 so I can choose 1⁄4 for c₁.

Finally, I have 1⁄4 * n² <= f(n) <= 1⁄2 * n² . This means that for a sufficiently large n, this routine is \Theta(n²).

About 0x0m03II

DevOps Engineer & Security Researcher

Email : 0x0m03II@thecodeguardian.dev

Website : http://thecodeguardian.dev